Hi,
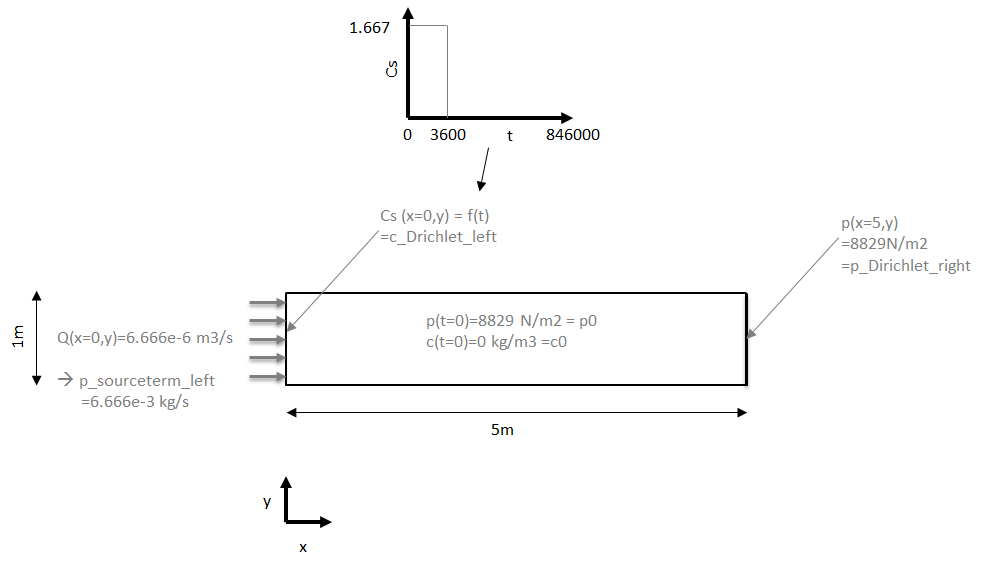
I have a model that should simulate 2d transport of an impulse load of a conservative hydraulic tracer through a 5m long (x) 1m wide (y) domain using the process ComponentTransport in ogs6.
IC of the pressure p0 is 8829 N/m2 on the domain.
There is a Dirichlet BC for the pressure at the outflow p(x=5,y) of p_Dirichlet_right=8829N/m2.
The water influx (Q) on the left side is implemented as a nodal source term p_sourceterm_left=6.666e-3 kg/s. I assumed the source term as mass flux according to the documentation of ComponentTransport.
The tracer component (name=Cs), has an IC of c0=0 and a temporal depending BC at the left side c_Drichlet_left to simulate the impulse injection from t=0 to t=3600s.
Total simulation time is 10 days (846000s).
The project file is here.
1st problem:
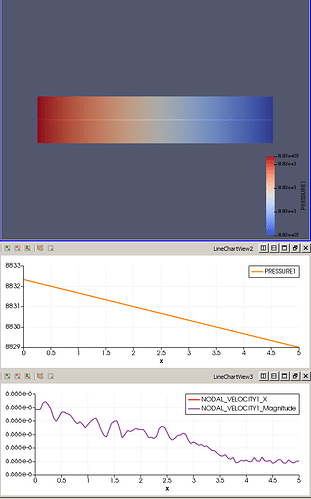
The simulation finishes however, the darcy_velocity outputted does not seem to be realistic.
I have a comparable model in ogs5, which works well (reliable velocity_x).
Here, the water flow is defiend via a source term on the left side and a Dirichlet condition for the pressure at the right side.
The tracer component conditions are similar as in the ogs6 example.
I already tried to implement the water mass influx as a Neumann BC (same value as for source term) in the ogs6 example, which yields the a similar darcy_velocity as in the ogs5 example. Fine.
My questions are:
Shouldn’t it work with defining the water influx as a nodal source term on the left boundary (ogs6)?
How is the nodal source term defined? I assumed it as mass per time (kg/s). However, this caused the unreliable darcy_velocity.
How is the neumann boundary condition defined? I assumed it as the derivative of the pressure, however, it seems to work well when I add the value of the water influx in kg/s. So, can you define mass fluxes using a Neumann BC?
I would appreciate your answer.
Best,
Johannes