Dear community developers and users,
Recently I’m working on applying OGS5 in ATES system. Before applying doublet in my model, I implemented one well at first to check if the model works well. In this basic model, the well is implemented in the middle of the domain. Besides, the domain size is 1000m x 1000m x 40m and the well is assigned as a polyline (from top to bottom). The water is injected into the well which is assigned as a flow rate (1e-3m3/s) in the source term (Neumann boundary condition) and a boundary condition (bc file) for temperature is assigned at the polyline to ensure the injected water temperature (16 degree Celsius). Moreover, the domain initial condition of temperature is 12 degree Celsius. All files applied in this model is given below in the zip file.
After the simulation, I tried to check if the energy in the system is equal to the energy injected into the system. The energy injected into the system can be calculated by: volume of injected water * (injected temperature - ambient temperature) * fluid specific heat capacity * fluid density. While for checking the energy in the system, I applied Paraview to integrate the temperature and domain volume. Firstly, the POINT_DATA_TO_CELL_DATA tool is used to convert the data type. Then the Calculator tool is applied to calculate the temperature deviation (baseline - 12 degree Celsius). And at the last, the Integrate_Variables is utilised to integrate the temperature deviation value and corresponding cell volume. Based on the result, the energy can be calculated by: Integration result * bulk volumetric heat capacity. The bulk volumetric heat capacity can be computed by: (solid specific heat capacity * solid density * (1- porosity) + fluid specific heat capacity * fluid density * porosity).
Finally, the relative energy error can be calculated with knowing exact injected energy and the increased energy in the system. The equation used here is: (Injected energy - Increased energy in the system) / Injected energy * 100 (%).
Result:
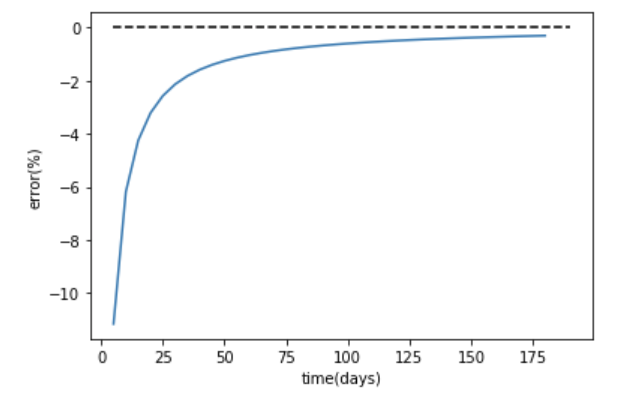
In the figure below, it is clearly that the initial relative error is quite large which indicates that the increased energy after the first time step is 10% more larger than the injected energy. This looks quite strange for me. Is there any reason for this phenomenon? Or do you have any recommendation in improving my model. Appreciate it for replying.
Best wishes,
Haoyue
Groundwater_Heat_transport.zip (1.6 MB)